Metropolis-Hastings

Author

Dr. Alexander Fisher

See libraries used in these notes 
library(tidyverse)
library(latex2exp)
library(patchwork)
library(tidymodels)
library(mvtnorm)
library(coda)
library(animation)

Notation

  • \(\theta\) is some parameter of interest.
  • \(\pi(\theta)\) represents the target distribution of the parameter.

Question: what does the phrase “explore parameter space” mean?

Metropolis algorithm

  1. Sample \(\theta^* | \theta^{(s)} \sim J(\theta | \theta^{(s)})\)
  2. Compute the acceptance ratio \(r = \frac{\pi(\theta^*)}{\pi(\theta^{(s)})}\)
  3. Let

\[ \theta^{(s+1)} = \begin{cases} \theta^* \text{ with probability } \min(r, 1)\\ \theta^{(s)} \text{ with probability } 1 - \min(r, 1) \end{cases} \]

Example 1

Let \(\pi(\theta) = \text{dnorm}(\theta, 10, 1)\) and let \(J(\theta | \theta^{(s)}) = \text{normal}(\theta^{(s)},\delta^2)\).

We have to choose \(\delta\). How should we choose it? Let’s gain some intuition by trying out three different values of \(\delta\).

set.seed(360)
theta_s = 0 # starting point
THETA = NULL # empty object to save iterations in
S = 10000 # number of iteations
delta = 1 # proposal variance
accept = 0 # keep track of acceptance rate

for (s in 1:S) {
  # log everything for numerical stability #
  
  ### generate proposal and compute ratio r ###
  theta_proposal = rnorm(1, mean = theta_s, sd = delta) 
  log.r = dnorm(theta_proposal, mean = 10, sd = 1, log = TRUE) - 
    dnorm(theta_s, mean = 10, sd = 1, log = TRUE)
  
  ### accept or reject proposal and add to chain ###
  if(log(runif(1)) < log.r)  {
    theta_s = theta_proposal
    accept = accept + 1 
  }
  THETA = c(THETA, theta_s)
}

Let’s look at a trace plot

df = data.frame(theta = THETA)
df %>%
  ggplot(aes(x = 1:nrow(df), y = theta)) + 
  geom_line() +
  theme_bw() +
  labs(x = "iteration", y = TeX("\\theta"))

Let’s look at how various \(\delta\) let us sample the target:

Example 2

The fledglings of female song sparrows. To begin, let’s load the data.

Load the data 
yX = structure(c(3, 1, 1, 2, 0, 0, 6, 3, 4, 2, 1, 6, 2, 3, 3, 4, 7, 
2, 2, 1, 1, 3, 5, 5, 0, 2, 1, 2, 6, 6, 2, 2, 0, 2, 4, 1, 2, 5, 
1, 2, 1, 0, 0, 2, 4, 2, 2, 2, 2, 0, 3, 2, 1, 1, 1, 1, 1, 1, 1, 
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
1, 1, 1, 3, 3, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 
2, 5, 5, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 5, 4, 4, 4, 4, 5, 
5, 5, 5, 3, 3, 3, 3, 3, 3, 3, 6, 1, 1, 9, 9, 1, 1, 1, 1, 1, 1, 
1, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 25, 25, 16, 16, 16, 16, 16, 
16, 16, 16, 16, 16, 16, 16, 25, 16, 16, 16, 16, 25, 25, 25, 25, 
9, 9, 9, 9, 9, 9, 9, 36, 1, 1), .Dim = c(52L, 4L), .Dimnames = list(
    NULL, c("fledged", "intercept", "age", "age2")))
yX %>%
  head(n = 5)
     fledged intercept age age2
[1,]       3         1   3    9
[2,]       1         1   3    9
[3,]       1         1   1    1
[4,]       2         1   1    1
[5,]       0         1   1    1
y = yX[,1]
X = yX[,-1]

The model:

\[ \begin{aligned} Y | X &\sim \text{Poisson}(\exp[ \beta^T \boldsymbol{x}])\\ \beta &\sim MVN(0, \sqrt{10}) \end{aligned} \]

The Metropolis algorithm with

\[ J(\beta | \beta^{(s)}) = MVN(\beta^{(s)}, \hat{\sigma}^2(X^TX)^{-1}) \]

where \(\hat{\sigma}^2\) is the sample variance of \(\{\log(y_1 + 1/2), \ldots, \log(y_n + 1/2)\}\).

Note
  • This variance is intuitively useful choice for \(\delta\) since the posterior variance would be \(\sigma^2 (X^TX)^{-1}\) in a normal regression problem.
  • We use \(\log(y + 1/2)\) instead of \(\log y\) because if \(y=0\), \(\log y\) would be \(-\infty\).
set.seed(360)
n = length(y)
p = ncol(X)

pmn.beta = rep(0, p) # prior mean beta
psd.beta = rep(10, p) # prior sd beta

var.prop = var(log(y + 1/2)) * solve(t(X) %*% X) # proposal variance

S = 10000
beta = rep(0, p); accepts = 0
BETA = matrix(0, nrow = S, ncol = p)
set.seed(1)

for (s in 1:S) {
  # multivariate proposal of beta
  beta.p = t(rmvnorm(1, beta, var.prop))
  
  # log ratio
  lhr = sum(dpois(y, exp(X %*%beta.p), log = TRUE)) -
    sum(dpois(y, exp(X %*% beta), log = TRUE)) + 
    sum(dnorm(beta.p, pmn.beta, psd.beta, log = TRUE)) -
    sum(dnorm(beta, pmn.beta, psd.beta, log = TRUE)) 
  
  if (log(runif(1)) < lhr) {
    beta = beta.p ; accepts = accepts + 1
  }
  
  BETA[s,] = beta
}

The acceptance ratio is 0.428

Let’s examine convergence.

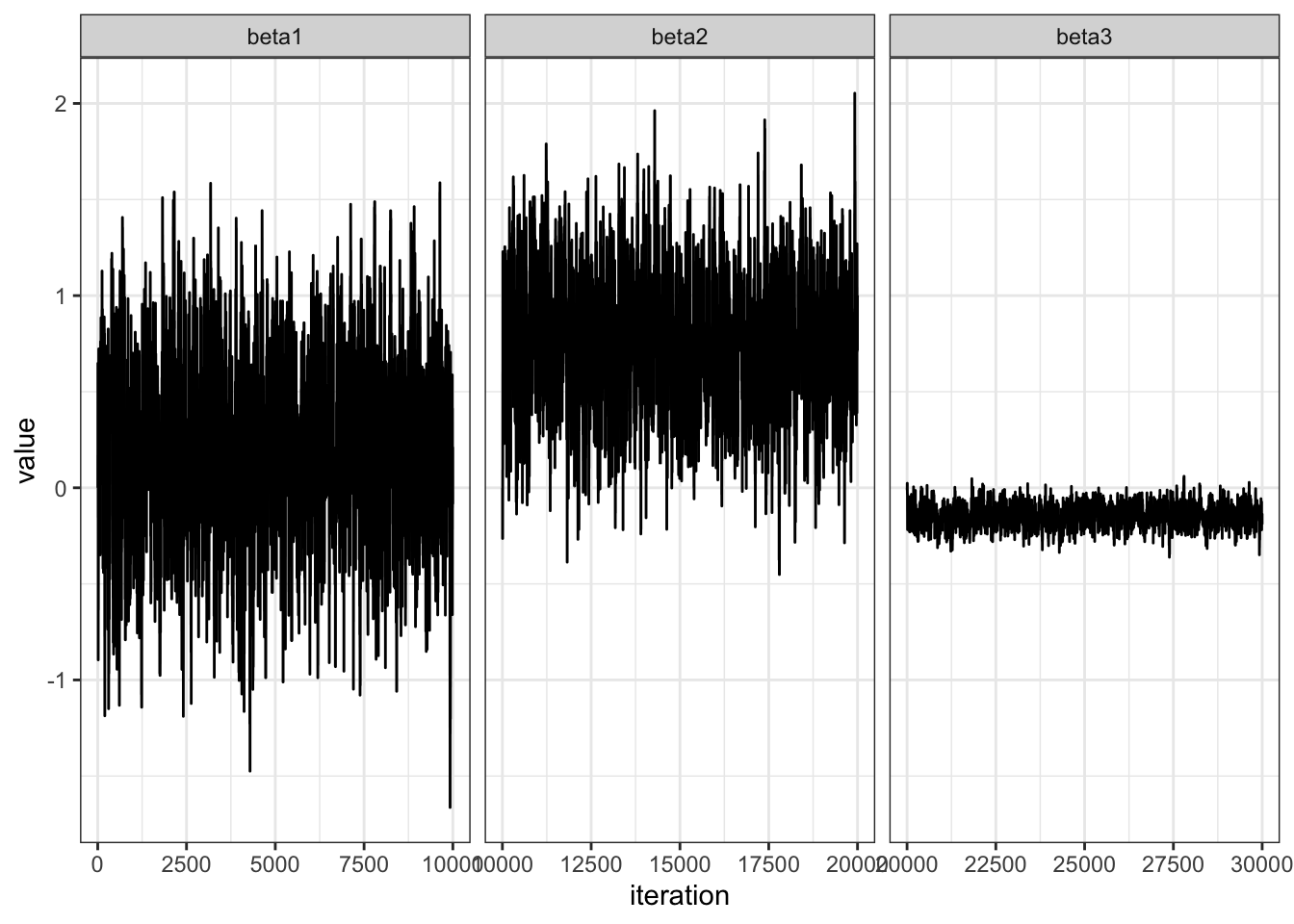
value = c(BETA[,1], BETA[,2], BETA[,3])
n = length(value)
beta = c(rep("beta1", n/3), rep("beta2", n/3), rep("beta3", n/3))
df = data.frame(value = value,
                beta = beta) 

df %>%
  ggplot(aes(x = 1:nrow(df), y = value)) + 
  geom_line() + 
  facet_wrap(~ beta, scales = "free_x") +
  theme_bw() +
  labs(x = "iteration")
# effective sample size
BETA %>%
  apply(2, effectiveSize)
[1] 867.4750 825.6214 692.0495
par(mfrow=c(1,3))
acf(BETA[,1])
acf(BETA[,2])
acf(BETA[,3])

Metropolis-Hastings

If we have a vector of parameters \(\theta = \theta_1, \ldots \theta_p\) then we can choose a proposal \(J(\theta | \theta^{(s)})\) that updates all \(\theta\) elements simultaneously (as seen above with \(J(\beta | \beta^{(s)})\).

Alternatively, we could update blocks of \(\theta\), e.g. propose an update for the first \(j\) elements of \(\theta\), \(J_1(\theta_1,\ldots \theta_j | \theta_1^{(s)}, \ldots \theta_j^{(s)})\) and then an update for the \(p-j\) remaining elements, \(J(\theta_{j+1}, \ldots, \theta_{p} | \theta_{j+1}^{(s)}, \ldots, \theta_{p}^{(s)})\).

Separately, we could even update each element of \(\theta\) individually, e.g. have an individual, different proposal on each \(\theta_i\), \(i \in \{1, \ldots p\}\).

We might even combine block updates with individual updates.

Question: Where have we seen block updates and individual updates within MCMC before?

The Metropolis-Hastings algorithm is a generalization of both the Metropolis algorithm and the Gibbs sampler.

The Metropolis-Hastings algorithm

Let \(\pi(\theta_1, \theta_2)\) be the target distribution. The Metropolis-Hastings algorithm proceeds:

  • Update \(\theta_1\):
  1. sample \(\theta_1^* \sim J_1(\theta_1 | \theta_1^{(s)}, \theta_2^{(s)})\);
  2. compute the acceptance ratio

\[ r = \frac{\pi(\theta_1^*, \theta_2^{(s)})}{\pi(\theta_1^{(s)}, \theta_2^{(s)})} \times \frac{J_1(\theta_1^{(s)}| \theta_1^*, \theta_2^{(s)})}{ J_1(\theta_1^{*}| \theta_1^{(s)}, \theta_2^{(s)}) } \]

  1. set \(\theta_1^{(s+1)}\) to \(\theta_1^*\) with probability \(\min(1, r)\), otherwise set \(\theta_1^{(s+1)}\) to \(\theta_1^{(s)}\).
  • Repeat the above to update \(\theta_2\) given \(\theta_1^{(s+1)}\).
Important

Here, the proposal distribution \(J\) need not be symmetric!