MCMC diagnostics practice

STA360 at Duke University

Exercises

Exercise 1

Let \(p(\theta_1, \theta_2 | \mathbf{y})\) be our target distribution, i.e. the distribution we are interested in sampling.

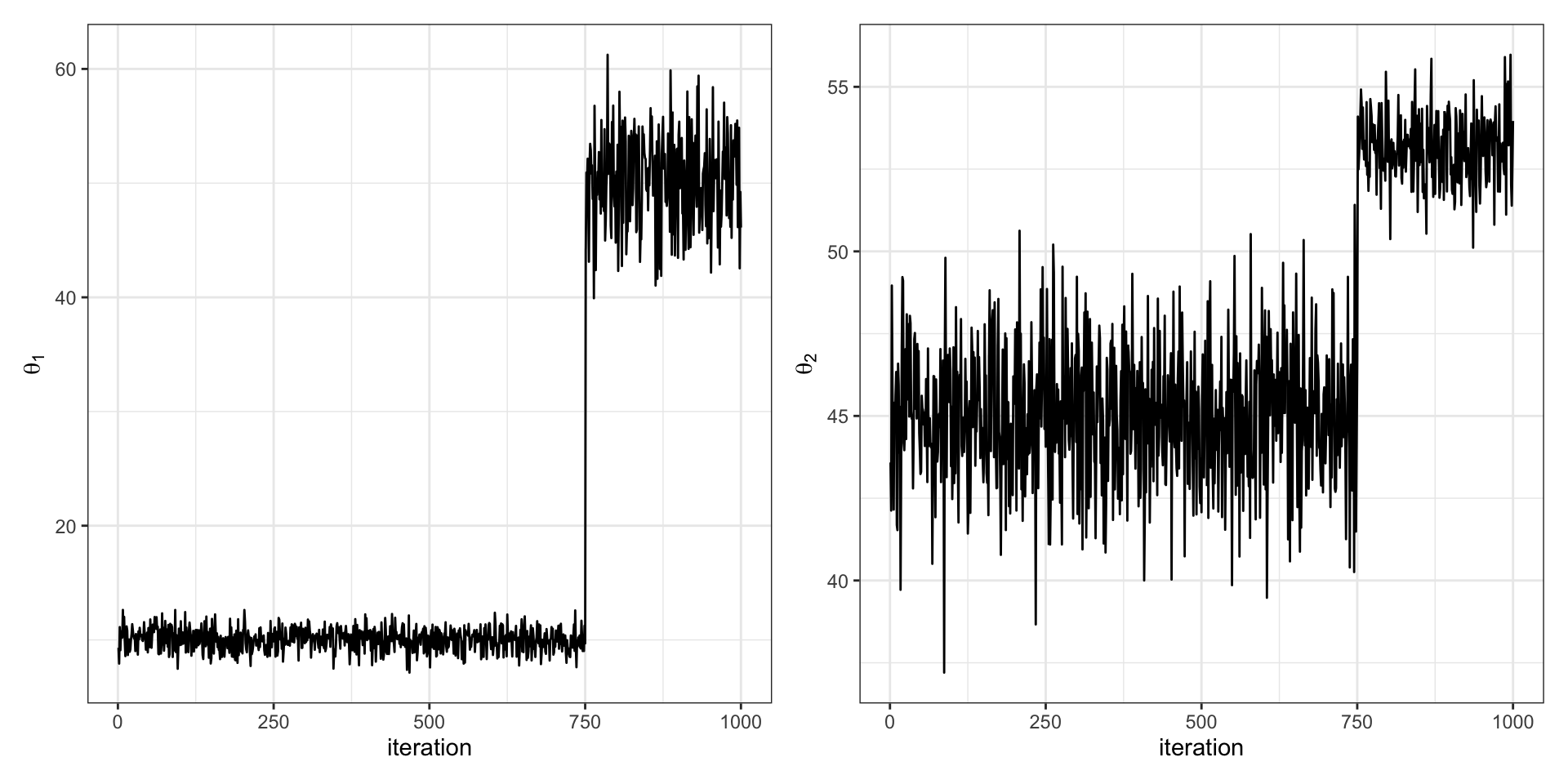
We construct a Gibbs sampler and look at the trace plots of \(\theta_1\) and \(\theta_2\), produced below. Chat with your neighbor, describe what you observe. Has the chain converged for each parameter? How well is the sampler mixing? Do you think the parameters are correlated or uncorrelated?

Write down a description of the plots below, in 2 paragraphs or less, for a reader who has not taken this class. You may assume the reader has taken a course on probability (e.g. similar to STA230/240).

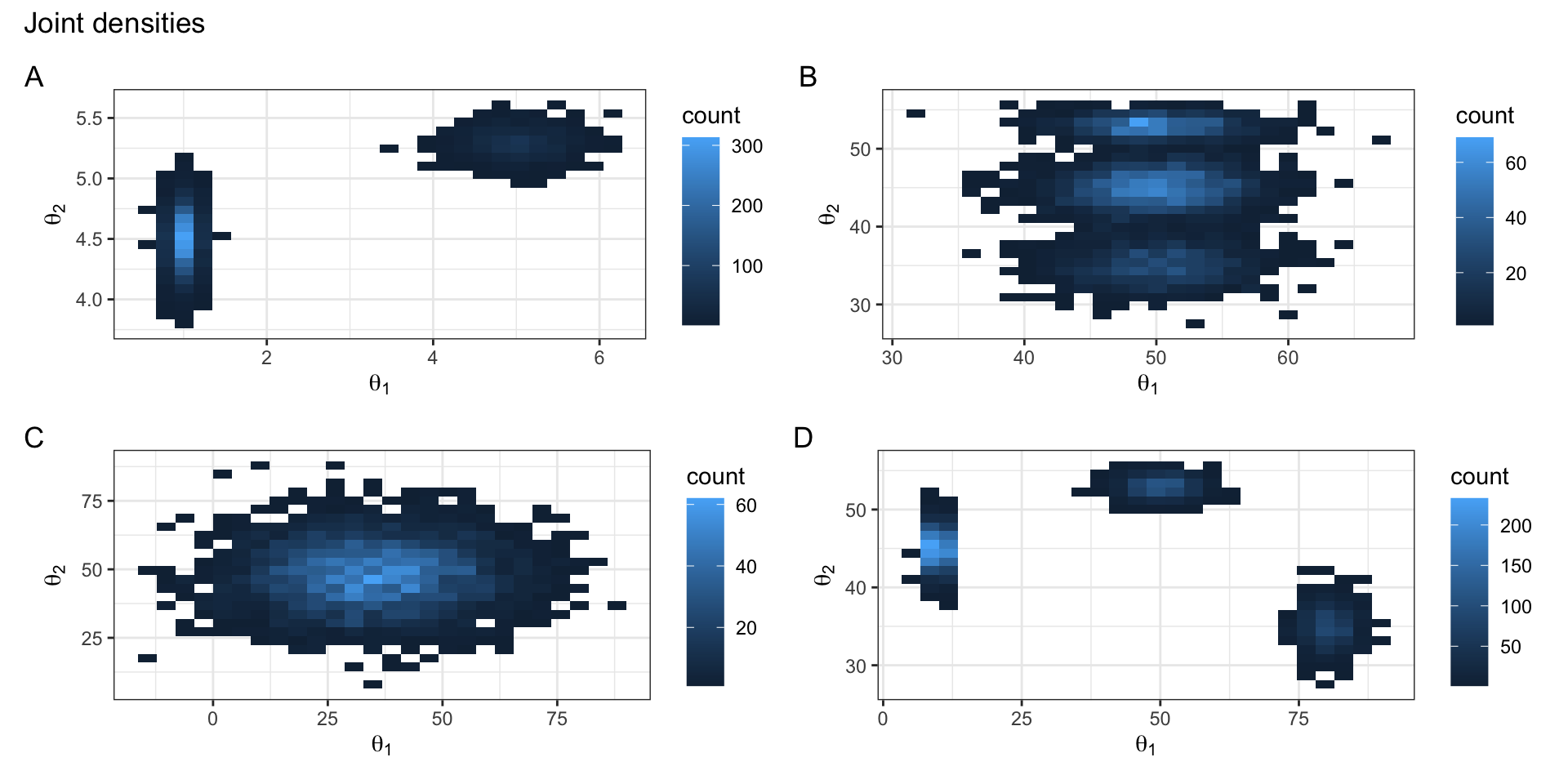
Exercise 2

Based on the first 1000 iterations of your Gibbs sampler shown on the previous slide, which of the following joint densities is the most plausible for \(\theta_1, \theta_2 | \mathbf{y}\)? Why? Hint: it may help to think about where your sampler starts and imagine a particle moving through space according to conditional updates.